Clustering With K-Means in Python
A very common task in data analysis is that of grouping a set of objects into subsets such that all elements within a group are more similar among them than they are to the others. The practical applications of such a procedure are many: given a medical image of a group of cells, a clustering algorithm could aid in identifying the centers of the cells; looking at the GPS data of a user’s mobile device, their more frequently visited locations within a certain radius can be revealed; for any set of unlabeled observations, clustering helps establish the existence of some sort of structure that might indicate that the data is separable.
Mathematical background
The k-means algorithm takes a dataset X of N points as input, together with a parameter K specifying how many clusters to create. The output is a set of K cluster centroids and a labeling of X that assigns each of the points in X to a unique cluster. All points within a cluster are closer in distance to their centroid than they are to any other centroid.
The mathematical condition for the K clusters and the K centroids
can be expressed as:
Minimize with respect to
.
Lloyd’s algorithm
Finding the solution is unfortunately NP hard. Nevertheless, an iterative method known as Lloyd’s algorithm exists that converges (albeit to a local minimum) in few steps. The procedure alternates between two operations. (1) Once a set of centroids is available, the clusters are updated to contain the points closest in distance to each centroid. (2) Given a set of clusters, the centroids are recalculated as the means of all points belonging to a cluster.
The two-step procedure continues until the assignments of clusters and centroids no longer change. As already mentioned, the convergence is guaranteed but the solution might be a local minimum. In practice, the algorithm is run multiple times and averaged. For the starting set of centroids, several methods can be employed, for instance random assignation.
Below is a simple implementation of Lloyd’s algorithm for performing k-means clustering in python:
import numpy as np
def cluster_points(X, mu):
clusters = {}
for x in X:
bestmukey = min([(i[0], np.linalg.norm(x-mu[i[0]])) \
for i in enumerate(mu)], key=lambda t:t[1])[0]
try:
clusters[bestmukey].append(x)
except KeyError:
clusters[bestmukey] = [x]
return clusters
def reevaluate_centers(mu, clusters):
newmu = []
keys = sorted(clusters.keys())
for k in keys:
newmu.append(np.mean(clusters[k], axis = 0))
return newmu
def has_converged(mu, oldmu):
return (set([tuple(a) for a in mu]) == set([tuple(a) for a in oldmu])
def find_centers(X, K):
# Initialize to K random centers
oldmu = random.sample(X, K)
mu = random.sample(X, K)
while not has_converged(mu, oldmu):
oldmu = mu
# Assign all points in X to clusters
clusters = cluster_points(X, mu)
# Reevaluate centers
mu = reevaluate_centers(oldmu, clusters)
return(mu, clusters)
Clustering in action
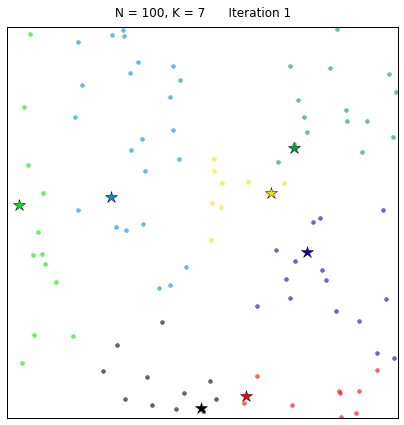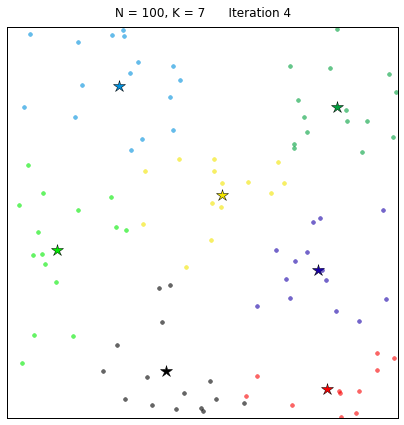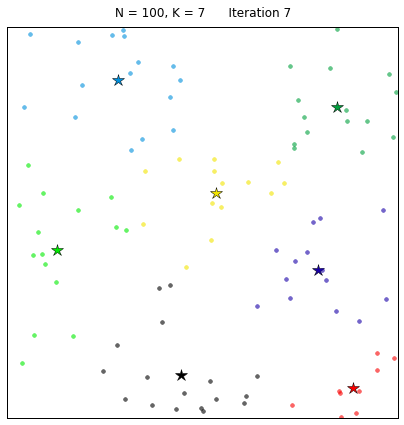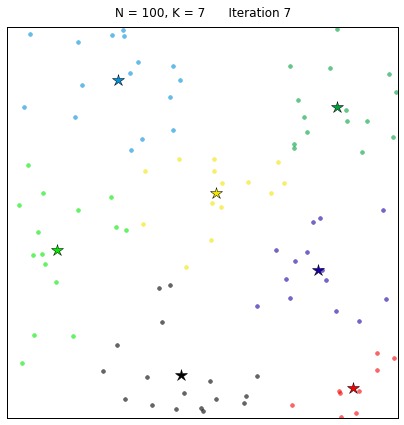
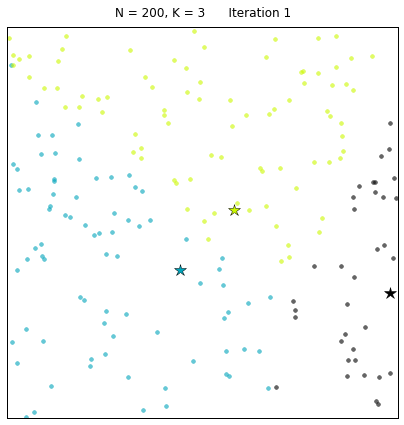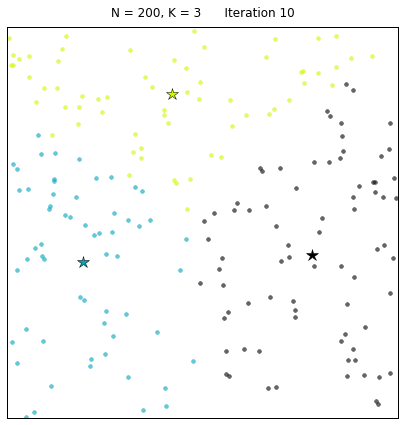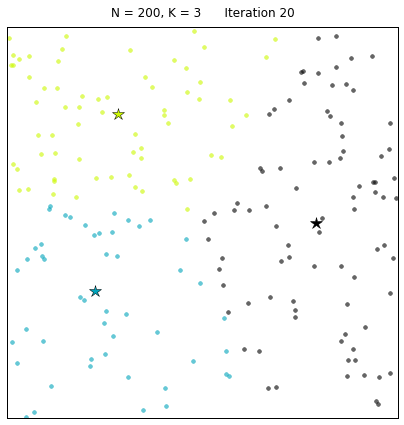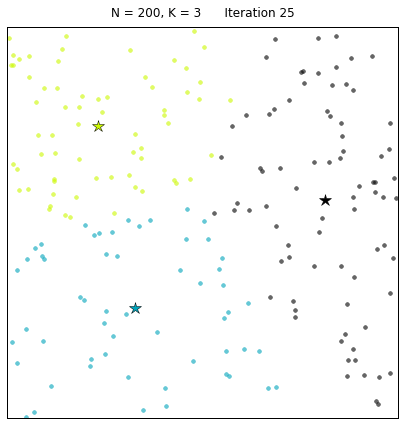
Let’s see the algorithm in action! For an ensemble of 100 random points on the plane, we set the k-means function to find 7 clusters. The code converges in 7 iterations after initializing with random centers. In the following plots, dots correspond to the target data points X and stars represent the centroids of the clusters. Each cluster is distinguished by a different color.
The initial configuration of points for the algorithm is created as follows:
import random
def init_board(N):
X = np.array([(random.uniform(-1, 1), random.uniform(-1, 1)) for i in range(N)])
return X
For a configuration with twice as many points and a target of 3 clusters, often the algorithm needs more iterations to converge.
Obviously, an ensemble of randomly generated points does not possess a natural cluster-like structure. To make things slightly more tricky, we want to modify the function that generates our initial data points to output a more interesting structure. The following routine constructs a specified number of Gaussian distributed clusters with random variances:
def init_board_gauss(N, k):
n = float(N)/k
X = []
for i in range(k):
c = (random.uniform(-1, 1), random.uniform(-1, 1))
s = random.uniform(0.05,0.5)
x = []
while len(x) < n:
a, b = np.array([np.random.normal(c[0], s), np.random.normal(c[1], s)])
# Continue drawing points from the distribution in the range [-1,1]
if abs(a) < 1 and abs(b) < 1:
x.append([a,b])
X.extend(x)
X = np.array(X)[:N]
return X
Let us look at a data set constructed as X = init_board_gauss(200,3): 7 iterations are needed to find the 3 centroids.
If the target distribution is disjointedly clustered and only one instantiation of Lloyd’s algorithm is used, the danger exists that the local minimum reached is not the optimal solution. This is shown in the example below, where initial data using very peaked Gaussians is constructed:
The yellow and black stars serve two different clusters each, while the orange, red and blue centroids are cramped within one unique blob due to an unfortunate random initialization. For this type of cases, a cleverer election of initial clusters should help.
To finalize our table-top experiment on k-means clustering, we might want to take a look at what happens when the original data space is densely populated:
The k-means algorithm induces a partition of the observations corresponding to a Voronoi tessellation generated by the K centroids. And it is certainly very pretty!
Table-top data experiment take-away message
Lloyd’s two-step implementation of the k-means algorithm allows to cluster data points into groups represented by a centroid. This technique is employed in many facets of machine learning, from unsupervised learning algorithms to dimensionality reduction problems. The general clustering problem is NP hard, but the iterative procedure converges always, albeit to a local minimum. Proper initialization of the centroids is important. Additionally, this algorithm does not supply information as to which K for the k-means is optimal; that has to be found out by alternative methods.
Update: We explore the gap statistic as a method to determine the optimal K for clustering in this post: Finding the K in K-Means Clustering and the method: Selection of K in K-means Clustering, Reloaded.
Update: For a proper initialization of the centroids at the start of the k-means algorithm, we implement the improved k-means++ seeding procedure.



I have been browsing online for over 4 hours today, but I haven’t found any interesting article like yours. In my opinion, if all site owners and bloggers write good articles like what you have done, the web will be a lot more useful than ever before.
You don’t have anything else to do, do you.
lol
Finally a blog on k-means with python without a “one-liner” scikit approach.
Just FYI: your objective function uses ||y – f(x)||, but that’s the norm, not the squared norm. So actually you’re implementing Lloyd’s for k-medians! It should be ||y – f(x)||^2. Great work anyway.
How to put these pictures out?
Excellent article. This is the first page that I come across not using sklearn.
I check your page every few days. A excellent article. You have the best ideas.
May I ask how did you get this animation effect of those points? Thanks a lot!
Awesome issues here. I am very glad to look your post.
Thank you so much and I am looking forward
to touch you. Will you please drop me a mail?
First, I’d like to congratulate for the post, it’s very didactic! But, I’m having trouble in execute your Lloyd’s Algorithm, specifically in the find_centers function. I tried in Python 3.6 (2017) and in 2.7 (2015) and both had gave me the same error:
def find_centers(X, K):
^
SyntaxError: invalid syntax
I’ve just copied the code and execute the program to see if it works. If anyone can help me on this problem I’ll be pleased.
Just missing a bracket in the previous statement.
where?thanks a lot
Have you solved your problem yet?I meet the same problem
there is an issue that I found: that code return either the k clusters or less than k while we want exactly k clusters. I think the problem is in cluster_points function.
I discovered your page on my Website feed. You have made my day! You already know this but you are someones reason to smile.
I am realy extremely pleased to visit your blog. Now I am found which I actually want.
I am very new to python and k-means. Can you please show me the code to visualize the results. thanks
—————————————————————————
TypeError Traceback (most recent call last)
in ()
2 K=3
3 X = init_board_gauss(N,K)
—-> 4 find_centers(X,K)
in find_centers(X, K)
2 # Initialize to K random centers
3 oldmu = random.sample(list(X), K)
—-> 4 mu = random.sample(X, K)
5 while not has_converged(mu, oldmu):
6 oldmu = mu
~\AppData\Local\Continuum\anaconda3\lib\random.py in sample(self, population, k)
312 population = tuple(population)
313 if not isinstance(population, _Sequence):
–> 314 raise TypeError(“Population must be a sequence or set. For dicts, use list(d).”)
315 randbelow = self._randbelow
316 n = len(population)
TypeError: Population must be a sequence or set. For dicts, use list(d).
Hi guys!
I am gettig this error when I tried to run this code on python3 environment. Can anyone help me sovle this error?
The find_centers function error is due to missing a parenthesis at the end of the line -> return (set([tuple(a) for a in mu]) == set([tuple(a) for a in oldmu])
The find_centers function error is due to missing a parenthesis at the end of the line -> return (set([tuple(a) for a in mu]) == set([tuple(a) for a in oldmu])
Buenas. La sección para cluster_point use (X,3) con X un conjunto de datos aleatorios y me lanza:
TypeError Traceback (most recent call last)
in ()
—-> 1 cluster_points(x,3)
in cluster_points(X, mu)
2 clusters = {}
3 for x in X:
—-> 4 bestmukey = min([(i[0], np.linalg.norm(x-mu[i[0]])) for i in enumerate(mu)], key=lambda t:t[1])[0]
5 try:
6 clusters[bestmukey].append(x)
TypeError: ‘int’ object is not iterable
Me pueden explicar si uso parametros errones y cuales debo utilizar
Hello
SEO Link building is a process that requires a lot of time fo wordpress.com
If you aren’t using SEO software then you will know the amount of work load involved in creating accounts, confirming emails and submitting your contents to thousands of websites in proper time and completely automated.
With THIS SOFTWARE the link submission process will be the easiest task and completely automated, you will be able to build unlimited number of links and increase traffic to your websites which will lead to a higher number of customers and much more sales for you.
With the best user interface ever, you just need to have simple software knowledge and you will easily be able to make your own SEO link building campaigns.
The best SEO software you will ever own, and we can confidently say that there is no other software on the market that can compete with such intelligent and fully automatic features.
The friendly user interface, smart tools and the simplicity of the tasks are making THIS SOFTWARE the best tool on the market.
IF YOU’RE INTERESTED, CONTACT ME ==> seosubmitter@mail.com
Regards,
Lemuel
how to implement the animation of clustering procedure?
I have the same issue but no one can answer
Thanks for sharing this information