Finding the K in K-Means Clustering
A couple of weeks ago, here at The Data Science Lab we showed how Lloyd’s algorithm can be used to cluster points using k-means with a simple python implementation. We also produced interesting visualizations of the Voronoi tessellation induced by the clustering. At the end of the post we hinted at some of the shortcomings of this clustering procedure. The basic k-means is an extremely simple and efficient algorithm. However, it assumes prior knowledge of the data in order to choose the appropriate K. Other disadvantages are the sensitivity of the final clusters to the selection of the initial centroids and the fact that the algorithm can produce empty clusters. In today’s post, and by popular request, we are going to have a look at the first question, namely how to find the appropriate K to use in the k-means clustering procedure.
Meaning and purpose of clustering, and the elbow method
Clustering consist of grouping objects in sets, such that objects within a cluster are as similar as possible, whereas objects from different clusters are as dissimilar as possible. Thus, the optimal clustering is somehow subjective and dependent on the characteristic used for determining similarities, as well as on the level of detail required from the partitions. For the purpose of our clustering experiment we use clusters derived from Gaussian distributions, i.e. globular in nature, and look only at the usual definition of Euclidean distance between points in a two-dimensional space to determine intra- and inter-cluster similarity.
The following measure represents the sum of intra-cluster distances between points in a given cluster containing
points:
.
Adding the normalized intra-cluster sums of squares gives a measure of the compactness of our clustering:
.
This variance quantity is the basis of a naive procedure to determine the optimal number of clusters: the elbow method.
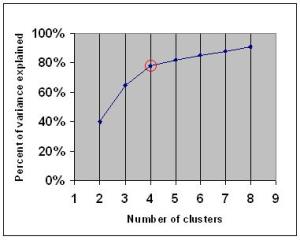
If you graph the percentage of variance explained by the clusters against the number of clusters, the first clusters will add much information (explain a lot of variance), but at some point the marginal gain will drop, giving an angle in the graph. The number of clusters are chosen at this point, hence the “elbow criterion”.
But as Wikipedia promptly explains, this “elbow” cannot always be unambiguously identified. In this post we will show a more sophisticated method that provides a statistical procedure to formalize the “elbow” heuristic.
The gap statistic
The gap statistic was developed by Stanford researchers Tibshirani, Walther and Hastie in their 2001 paper. The idea behind their approach was to find a way to standardize the comparison of with a null reference distribution of the data, i.e. a distribution with no obvious clustering. Their estimate for the optimal number of clusters
is the value for which
falls the farthest below this reference curve. This information is contained in the following formula for the gap statistic:
.
The reference datasets are in our case generated by sampling uniformly from the original dataset’s bounding box (see green box in the upper right plot of the figures below). To obtain the estimate we compute the average of
copies
for
, each of which is generated with a Monte Carlo sample from the reference distribution. Those
from the
Monte Carlo replicates exhibit a standard deviation
which, accounting for the simulation error, is turned into the quantity
.
Finally, the optimal number of clusters is the smallest
such that
.
A Python implementation of the algorithm
The computation of the gap statistic involves the following steps (see original paper):
- Cluster the observed data, varying the number of clusters from
, and compute the corresponding
.
- Generate
reference data sets and cluster each of them with varying number of clusters
. Compute the estimated gap statistic
.
- With
, compute the standard deviation
and define
.
- Choose the number of clusters as the smallest
such that
.
Our python implementation makes use of the find_centers(X, K) function defined in this post. The quantity is computed as follows:
def Wk(mu, clusters):
K = len(mu)
return sum([np.linalg.norm(mu[i]-c)**2/(2*len(c)) \
for i in range(K) for c in clusters[i]])
The gap statistic is implemented in the following code snapshot. Note that we use for the reference datasets and we span values of
from 1 to 9.
def bounding_box(X):
xmin, xmax = min(X,key=lambda a:a[0])[0], max(X,key=lambda a:a[0])[0]
ymin, ymax = min(X,key=lambda a:a[1])[1], max(X,key=lambda a:a[1])[1]
return (xmin,xmax), (ymin,ymax)
def gap_statistic(X):
(xmin,xmax), (ymin,ymax) = bounding_box(X)
# Dispersion for real distribution
ks = range(1,10)
Wks = zeros(len(ks))
Wkbs = zeros(len(ks))
sk = zeros(len(ks))
for indk, k in enumerate(ks):
mu, clusters = find_centers(X,k)
Wks[indk] = np.log(Wk(mu, clusters))
# Create B reference datasets
B = 10
BWkbs = zeros(B)
for i in range(B):
Xb = []
for n in range(len(X)):
Xb.append([random.uniform(xmin,xmax),
random.uniform(ymin,ymax)])
Xb = np.array(Xb)
mu, clusters = find_centers(Xb,k)
BWkbs[i] = np.log(Wk(mu, clusters))
Wkbs[indk] = sum(BWkbs)/B
sk[indk] = np.sqrt(sum((BWkbs-Wkbs[indk])**2)/B)
sk = sk*np.sqrt(1+1/B)
return(ks, Wks, Wkbs, sk)
Finding the K
We shall now apply our algorithm to diverse distributions and see how it performs. Using the init_board_gauss(N, k) function defined in our previous post, we produce an ensemble of 200 data points normally distributed around 3 centers and run the gap statistic on them.
X = init_board_gauss(200,3) ks, logWks, logWkbs, sk = gap_statistic(X)
The following plot gives an idea of what is happening:

The upper left plot shows the target distribution with 3 clusters. On the right is its bounding box and one Monte Carlo sample drawn from a uniform reference distribution within that rectangle. In the middle left we see the plot of that is used to determine
with the elbow method. Indeed a knee-like feature is observed at
, however the gap statistic is a better way of formalizing this phenomenon. On the right is the comparison of
for the original and averaged reference distributions. Finally, the bottom plots show the gap quantity on the left, with a clear peak at the correct
and the criteria for choosing it on the right. The correct
is the smallest for which the quantity plotted in blue bars becomes positive. The optimal number is correctly guessed by the algorithm as
.
Let us now have a look at another example with 400 points around 5 clusters:
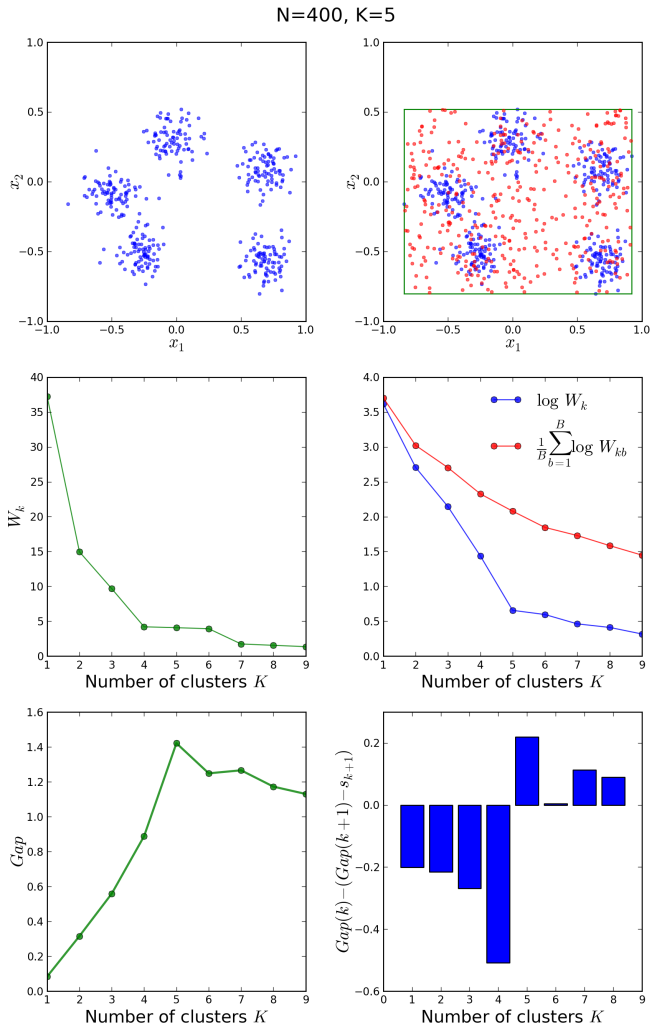
In this case, the elbow method would not have been conclusive, however the gap statistic correctly shows a peak in the gap at and the bar plot changes sign at the same correct value.
Similarly, we can study what happens when the data points are clustered around a single centroid:
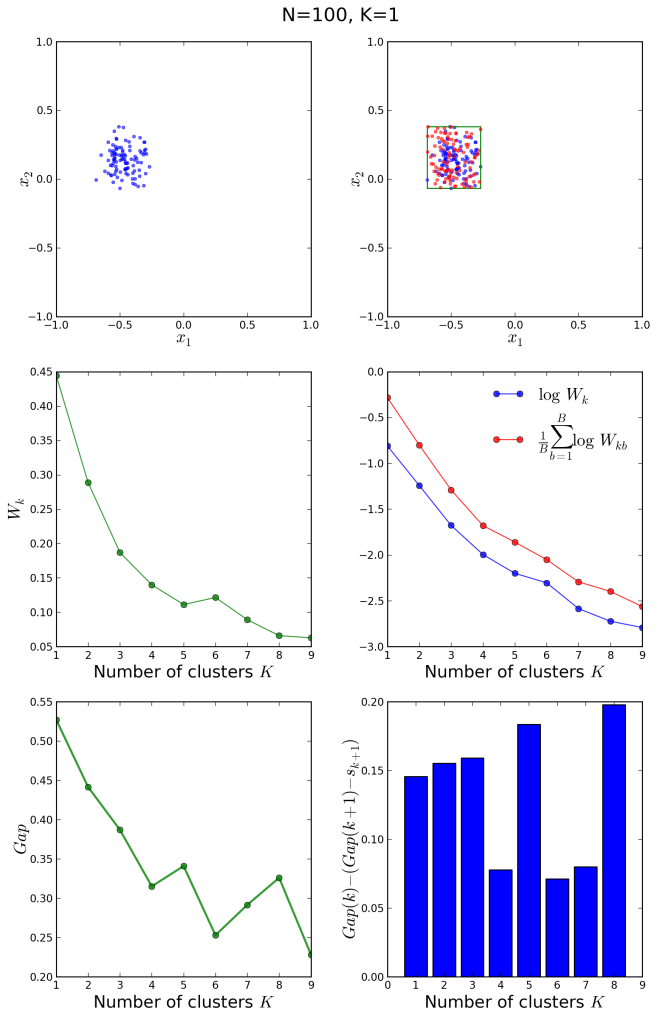
It is clear in the above figures that the original and the reference distributions in the middle right plot follow the same decay law, so that no abrupt fall-off of the blue curve with respect to the red one is observed at any . The bar plot shows positive values for the entire
range. We conclude that
is the correct clustering.
Finally, let us have a look at a uniform, non-clustered distribution of 200 points, generated with the init_board(N) function defined in our previous post:
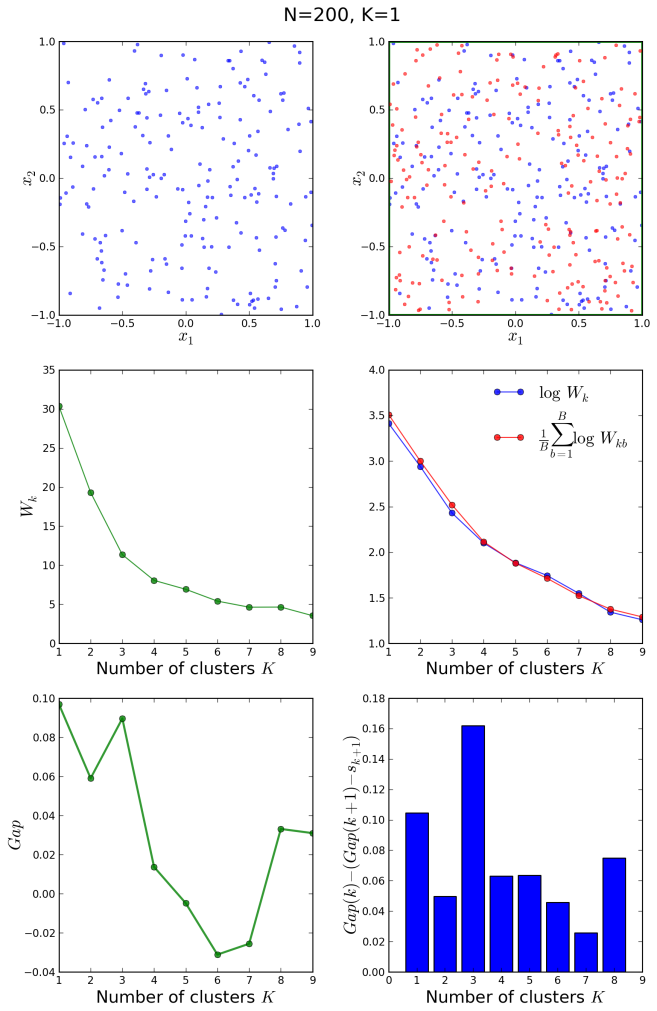
In this case, the algorithm also guesses correctly, and it is clear from the middle right plot that both the original and the reference distributions follow exactly the same decay law, since they are essentially different samples from the same uniform distribution on [-1,1] x [-1,1]. The gap curve on the bottom left oscillates between local maxima and minima, indicating certain structures within the original distribution originated by statistical fluctuations.
Table-top data experiment take-away message
The estimation of the optimal number of clusters within a set of data points is a very important problem, as most clustering algorithms need that parameter as input in order to group the data. Many methods have been proposed to find the proper , among which the “elbow” method offers a very clear and naive solution based on intra-cluster variance. The gap statistic, proposed by Tobshirani et al. formalizes this approach and offers an easy-to-implement algorithm that successfully finds the correct
in the case of globular, Gaussian-distributed, mildly disjoint data distributions.
Update: For a proper initialization of the centroids at the start of the k-means algorithm, we implement the improved k-means++ seeding procedure.
Update: For a comparison of this approach with an alternative method for finding the K in k-means clustering, read this article.
Reblogged this on .
There is a very clear discussion on the gap statistic as well as a link to an R implementation of the algorithm at http://blog.echen.me/2011/03/19/counting-clusters/
The link has failed…
Thank you for this very clear discussion. One drawback of this method is that calculation of the gap statistic requires a monte carlo simulation. There is a version of this approach that uses a closed form approximation of the reference distribution, which can be much faster an probably almost as good: http://www.ee.columbia.edu/~dpwe/papers/PhamDN05-kmeans.pdf
That’s a great reference, thanks! And now I feel like coding up the Pham et al. approach and see how it performs vs. the gap statistic. Will keep you posted 😉
I finally found the time to implement your suggested approach, and it was fun! https://datasciencelab.wordpress.com/2014/01/21/selection-of-k-in-k-means-clustering-reloaded/
Thanks for the reference!
Hi
k means is a simple yet powerful tool. I have been using it to classify stocks into groups for statistical arbitrage. The choice of K was largely determined by the fundamental interpretations of the resulting clusters. I have shown a simple application on the usefulness of K means in classification posted on my blog:
http://quantcity.blogspot.in/2014/05/k-means-clustering-based-stock.html
The elbow method that you have discussed here is very interesting. I would definitely attempt your approach to see if it improves the performance of our trading systems. Thanks for the post. Very informative.
Little confused, should not the division by 2 * len(c) be suppressed ?
That factor corresponds to the 1/(2*n_k) present in the definition of W_k (see the formula above for W_k); n_k is the number of elements of each cluster, so it can be computed as the length of the array c for every element c in clusters.
Thanks for the response.
Yes, but does not numpy norm calculates the square-root of sum of square of every pair of points. So that the in the formula you don’t need to muliply 2* len_of_cluster. i.e. it is calculating the first equal of the formula for Dk, not the second one as mentioned.
Posting this as I feel the previous comment didn’t came out clear enough.
In the formula for Dk there is a factor of 2*len_of_cluster which is mulitplied to norm. Now as the numpy norm is calculating the same norm. Either we need to multiply 2*len_of_cluster and divide later. Or you can simply ignore the division by the 2*len_of_cluster.
Please correct my if I am wrong or I understood anything incorrectly.
I’m totally agree with you, here c is just a single point in a cluster, for 2d point, len(c) is always 2, from the reply of author, he considered c as a cluster, but it isn’t from the source code, i think the right code is
sum([np.linalg.norm(mu[i]-x)**2 for i in range(K) for x in clusters[i]])
I agree with the previous comments.
If the “second” version of the inter cluster distances are used where the sum is the squared distance of every observation to the mean * the number of observations * 2. Then this is surely cancelled out when this is inserted into the W_k formula. Correct?
Gap(k) = Wkbs[indk] – Wks[indk]
From magazines to website content to social media posts, people need to write great content if they want to attract people. I was riding my bike on Thursday when I heard about this. What’s really great about your website is that it provides really valuable data and is also being entertaining. Not everyone is great at thinking outside of the box and still being detail oriented. Some really excellent info here.
I ran this algorithm but the resulted K varies each time I ran it. Most of time it will be stable around a reasonable value but it can exceed the max possible K(10) I set. Is it normal? (I used kmeans ++ for initial centroids)
same here, and I wonder how could we really use that ‘optimal’ k value if it changes every time
I used Gap statistics with Pam and found satisfactory results.
Question about the B parameter, I understand that this determines the size of the Monte Carlo. Is there any reason why more wouldn’t be better here (outside of computation cost)?
Reblogged this on leishu2blog.
Reblogged this on Educational Data Mining (EDM) and You!.
I did not go through this in detail. A quick question though…out of the four return values [ks, logWks, logWkbs, sk = gap_statistic(X)], which one gives the gap-value (or the optimal K value)?
Hey,
Thanks for such a resourceful article.
I have a confusion I want to clear. I clustered a research paper database with their abstracts, titles, names and authors.
I used k-means to cluster for word-count purpose. The output is very odd.
“`
cluster 0: 3530 papers
cluster 1: 1 papers
cluster 2: 1 papers
Within Set Sum of Squared Errors = 2.3246721652594484E7
“`
I repeated this for k=3 to k=35, but the results were similar.
Belief: I believe this data is spherically aligned.
The WSSSE does not change much from 2.15 to 2.32. Elbow method does not work on its graph.
I did not apply GAP method on it as it was just for project purposes.
Does it mean what I think or would GAP method will help
When I feed this function my data as a numpy array, I get this error:
TypeError: Population must be a sequence or set. For dicts, use list(d).
what am I doing wrong?
thanks
You need to convert your numpy array (an ndarray) to a list. The easiest way is using the tolist() function provided by the array itself, i.e.: your_array.tolist()
Hi, Can I try this on a dataframe? a pandas df? I tried but it throws list error!
nice blog and very useful post! check mine at http://dzenanhamzic.com
Hi,
I got the same error as “May 9, 2016 – 6:05 pm Anonymous”. When I convert tolist() as suggested I get
TypeError: unsupported operand type(s) for -: ‘list’ and ‘list’
Cheers
Marc
And actually I get the same if I use X=init_board_gauss(200,3)
Cheers
Was this issue resolved @marc&Ramona?
Nope, in the meantime I focused on something else…… probably to do with the installation. Currently I get the error
File “C:\Program Files\Anaconda3\lib\random.py”, line 311, in sample
raise TypeError(“Population must be a sequence or set. For dicts, use list(d).”)
TypeError: Population must be a sequence or set. For dicts, use list(d).
There is an explicit formula associated with the elbow method to automatically determine the number of clusters. You can find it in my article, at https://dsc.news/2EYkh3E
I was never one to obsess with what my wedding dress
would look like until the day came when I would marry the man of my dreams.
I had a lot of varied ideas and varied styles that I was in love with and it definitely had
to have some sparkle and bling! Being a plus size bride gives
little of that variety available, and unless you have a wealthy
bank account, that dream dress can seem unattainable!
My first experience with Brilliant Bridal was open-minded.
I really didn’t know what to expect and was hoping for something that was not
outdated and financially obtainable. I had the pleasure of working
with Helen, and she was so cheerful, helpful and willing to do what it took
to see my needs were met. There was a good variety of beautiful, and elegant dresses
in my size and I knew I was in the right place.
I was so incredibly happy with the outcome of this experience.
I was able to find \ https://smartsheet.com
en kaliteli filmler senin için